Football Predictions Overview

Football (soccer) is one of the most popular sports in the world, and despite being quite unpredictable sometimes, is also one of the top betting markets. It is no surprise that tremendous efforts have been put into developing models to predict the outcome of football games. Most of those models use historical data as the basis for the prediction. For example, the number of previous wins/loses determines the probability of a team winning, drawing, or losing today; or the number of goals scored/allowed over a period of time can be used to predict future scores. In that context, we can use Microsoft Excel to gather and visualize such data, and to easily calculate outcome probabilities and goal estimates.

Outcome Probabilities

Probabilities are numerical descriptions of the likelihood of an event happening. In football, three possible events can occur: win, draw, or loss (also referred as 1X2). Regardless of the team’s specific strengths and weaknesses, the winning probability represents the ultimate fundamental measure of team success (win potential).

There are many different ways to compute probabilities for each possible outcome using past data. In the most simplistic approach, we can find previous results for the exact two teams and forecast the next confrontation (known as head-to-head). For example, see below the games played between Real Madrid (playing home) and Barcelona (visitor) in the Spanish regular league Primera Division (La Liga) for the last 20 years.

We can easily reconcile basic stats as shown in the table below (taken from the Excel Football Statistics Dashboard). Real Madrid faced Barcelona 20 times at home, it won 7 games, drew 3 and lost 10. That gives Real Madrid a winning probability of 35% over Barcelona, while losing is more probable (50%) and drawing seems quite unlikely (15%). However, even if we could speculate with those numbers, the data spans over the last 20 years and, therefore, the stats may not reflect the current situation.

Let’s see another example. Real Madrid played home against Atletico Madrid 17 times over the last 20 years (see stats below). It seems that Atletico, as visitor, has a very low probability (11.8%) to beat Real. But again, the sample is small and spans over many years, so it may not be representative enough to make any realistic prediction. Teams experience change over time (players, coach, strategy, etc.) and can perform different to what it was expected based on earlier scenarios. Therefore, head-to-head stats, despite being useful in certain situations, have to be taken with caution.

It is then reasonable, and well known, the fact that using more recent data generally improves the predictions. But in some cases we may not have sufficient records available, sometimes there aren’t even any games at all to compare (teams never played each other before). One way to overcome this limitation is to calculate adjusted figures based on overall team’s outcome probabilities.

Let’s have a look at Real Madrid’s games played home during the last season (2019-2020) in the table below. Similar to what we did earlier with head-to-head stats, we can easily reconcile the probability for each outcome. Real Madrid won 15 games out of 19 playing home in 2019-2020; its overall winning percentage is 78.9%.

We have done the same calculation for each team in the Spanish Primera Division league playing home and away during the previous season (2019-2020). See the outcome (W/D/L) probabilities in the summary table below, which is a simple Excel pivot table with calculated fields (explained in this other article: Excel Football Statistics Dashboard).

With those figures, we can calculate adjusted probabilities for Real Madrid (Home) vs Barcelona (Away) as the average of opposed probabilities multiplied by the sample size (number of games played).

Real Madrid win probability = (78.9% × 19 + 26.3% × 19) / 38 = 52.6%

As the number of games is the same for Real Madrid playing home and Barcelona playing away, we can simplify the equation and just compute the arithmetic mean of home win and away lose probabilities:

Real Madrid win probability = (78.9% + 26.3%) / 2 = 52.6%

 

Similarly, we can calculate draw and loss probabilities for Real Madrid vs Barcelona as follows:

Real Madrid-Barcelona draw probability = (21.1% + 26.3%) / 2 = 23.7%

Real Madrid loss probability (Barcelona wins) = (0% + 47.4%) / 2 = 23.7%

These probabilities look quite different to what we’ve seen earlier using head-to-head stats over the last 20 years, and possibly reflect better the current win/lose potential for each team. It is common practice to use data from the previous season (sometimes the last 2 or 3 seasons) to forecast the following new season. In some cases, the last 3 or 5 games played give more precise information for certain parameters.

But can these simple estimates be used to make any predictions at all? We have calculated outcome probabilities for all games in recent seasons (pre-covid) for three major European leagues, using previous season’s data to make predictions within the following season. We have observed a 47-58% chance to guess the right outcome (1X2) when picking the highest estimate percentage. The success percent was noticeably higher for the English Premier League. Setting a threshold (e.g. 42% to predict a home win) instead of just picking the highest percent, or using some strategies to favor the draw, could improve the predictions. Thus, we can claim that, despite its simplicity, this method provides some useful information about the expected outcome. With that being said, it is also important to highlight that these outcome predictions can be further improved using the Poisson model discussed in this other article: Football Predictions with Poisson Distribution.

Goal Estimates

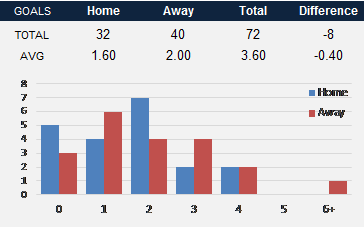
In the first example we’ve seen head-to-head stats for Real Madrid (home) vs Barcelona (away) over the last 20 years. During that time, Real Madrid scored 32 goals and allowed 40 to Barcelona. We could say Real scored on average 1.6 goals and allowed 2.0 per game against Barcelona. The goal distribution is shown below as the frequency for each goal outcome.

As explained earlier, these figures span over a long period and may not represent the current situation; we need to look at more recent data in order to improve the predictions.

Let’s then have a look at the average number of goals scored and allowed in the previous season (2019-2020), which is the number of goals scored/allowed divided by number of games played (see GF and GA in the summary table presented earlier). Real Madrid scored an average of 2.11 goals per game and allowed 0.58 when playing home in 2019-2020. Barcelona scored 1.79 per game and allowed 1.16 when playing away. The average number of goals scored and allowed is generally weighted against the average league/season goals to calculate what’s commonly known as the attack and defensive strength of a team. The average league goals scored and allowed in 2019-2020 was 1.44 and 1.04 respectively. With those figures, we can now calculate the expected number of goals for Real Madrid vs Barcelona as the product of home and away average goals scored/allowed divided by league average goals scored/allowed:

Real Madrid’s (home) goal estimate = (2.11 × 1.16) / 1.44 = 1.70 goals

Barcelona’s (away) goal estimate = (1.79 × 0.58) / 1.04 = 1.00 goals

Based on the difference, we would expect Madrid to score more goals than Barcelona; if we round the numbers, we could guess the final score to be somewhere around 2-1. But the difference is not significant enough to drive any conclusion. Furthermore, we all know football is not that predictable and anything can happen. So, can we really get anything out of these estimates?

We have calculated goal estimates for all games in recent seasons (pre-covid) for three major European leagues using previous season’s data. Then we used the goal estimates to predict the outcome and score of games in the following season. For each game, the expected winner is the team with a higher goal estimate (when rounding the numbers or using other trivial approximations). When the goal estimates are too close we expect a draw. We have observed a poor correlation between the predictions based on goal estimate differences and the real outcome. Similarly, we rounded the estimates to predict the goals and final score. The rounded estimates were found to get right between 26-35% of home goals, 35-41% of away goals, 18-29% of total goals, and 9-17% of final scores. Bottom line, these estimates give a rough idea but are not sufficient to anticipate any particular result.

The goal expectancy estimates calculated here can be computed into statistical models to get the probability for different goal outcomes. One of the most common statistical models used in football is the Poisson distribution discussed in this other article: Football Predictions with Poisson Distribution.

 

Additional Considerations

There are numerous variables that have an impact on the final outcome and score of a game, and therefore should be included in the predictive models. For example, ball possession time is often relevant, as the longer the team keeps the ball, usually, the higher the chance to win (although not necessarily to score more goals than expected). The playing style is also important, and is somehow linked to the possession time. Certain playing styles may favor scoring, while others suggest fewer goals or draw. The number of overall shots and shots on target are also important factors to consider. The more the number of shots, the more likely is the team to score. More recently, and with more data available, the location of shots in the field has been added to models and found to improve some predictions.

Additionally, factors on a broader scope can be relevant in certain situations and should also be considered in the models. Among others, the form and position in the standings (determined by the team’s points) and average number of points per game, can influence fundamental factors such as possession and playing style, which may affect the expected outcome. That could happen for example when two teams are tight in the table and want to gain the position at any cost, or if one of the teams is at the bottom and decides to change strategy, maybe risking more or playing more aggressively thus leading to more goals than expected. Another interesting observation is that pre-season and early season games are quite different than late/end of season, so the number of rounds played may have an effect on predictions too. It is also important to understand the type of tournament we are modelling (regular season, championship, cup) and analyze relevant past data accordingly.

Finally, some particular unusual situations with no previous records may occasionally have a significant impact and need to be considered in the predictions. Some of these include injuries or disqualified players, climatological conditions, psychological factors, socio-economic situation of the club, etc.